Limites de fonctions

I. Limite finie ou infini en +∞ ou -∞ :

A. Limite infinie en +∞ ou -∞

Définitions

f a pour limite +∞ en +∞ signifie que

pour tout intervalle J = ] A ;+∞ [ A un réel, il existe un réel a assez grand tel que pour tout x >a, f(x) appartient à J.

f a pour limite -∞ en +∞ signifie que que -f a pour limite +∞ en +∞.

Exemples :

Fonctions de référence

lim x =+∞ . . . . lim xⁿ =+∞ avec n un entier naturel non nul ….......lim e^x = +∞

x→+∞...............x→+∞.......................................................................x→+∞

B. Limite finie en +∞ ou -∞

Définitions :

Dire qu'une fonction f tend vers j un réel, lorsque x tend vers +∞(resp. -∞), signifie que tout intervalle ouvert J contenant j, il existe A (resp. B) un réel assez grand tel que tout x > A (resp. x<B) , f(x) appartient à J.

On note lim f(x) =j

…..........x→+∞

Exemples :

Fonctions de référence

lim e^x = 0...........lim x^-n =0 avec n un entier naturel non nul

x→-∞................ x→+∞

Interprétation graphique :

On dit dans ce cas que Cf admet une asymptote horizontale d'équation y=j

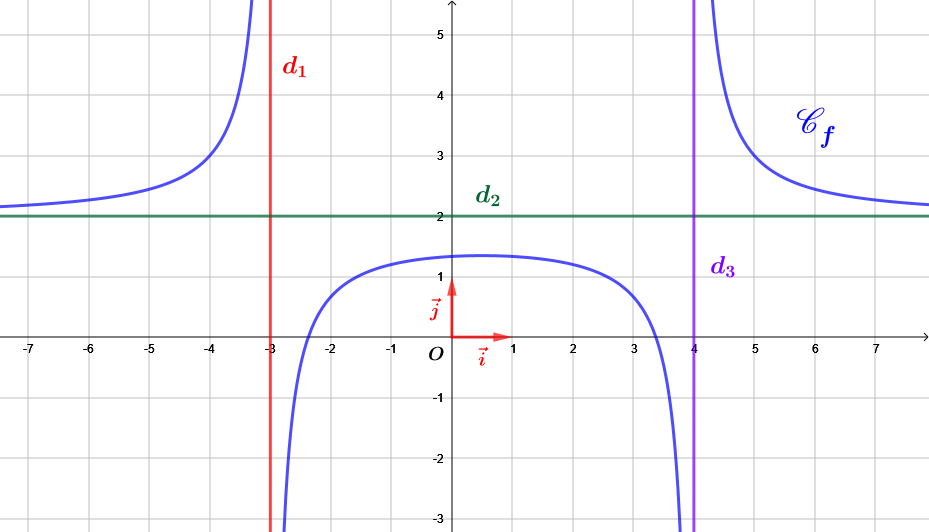
Sur le graphique ci-dessus lim f(x) =2, on dit que la droite d2 d'équation y=2 est une asymptote horizontale à Cf

^{….....................................................x→+∞}

II. Limite finie ou infinie en a

A. Limite infinie en a

Définitions :

Dire qu'une fonction f tend vers +∞ lorsque x tend vers a, signifie que tout réel j et pour tout x assez proche de a on a f(x) > j.

On note lim f(x) =+∞

..............x→a

On dit dans ce cas que Cf admet une asymptote verticale d'équation x=a

Sur le graphique ci-dessus Cf admet une asymptote verticale d'équation x=4 car

lim f(x) =+∞ on dit que f a pour limite +∞ à droite de 4 on note aussi lim f(x) =+∞,

x→4^{+.................................................................................................................................................}x→4

^{...............................................................................................................................................................................................}x>4